负荷能力
了解 Smalley 弹性挡圈装置的承载能力需要对挡圈剪切和凹槽变形进行计算,设计限制取其中的较小者。 负荷能力公式不会考虑动态或偏心负荷。 如果存在这种负载,就应该应用适当的安全因素并进行产品测试。 此外,应考虑凹槽几何结构和边缘间隙 。 如果存在恶劣的工作条件,实际挡圈性能最好通过实际的测试来确定。
挡圈剪切
 虽然通常不视为 Smalley 弹性挡圈的典型故障,但在将硬化钢用作凹槽材料时,挡圈剪切可能是一个设计限制。 我们的标准挡圈表中提供了基于挡圈剪切的挡圈轴向负荷能力。 这些值基于建议安全因子为 3 的碳素钢的 剪切强度 。
虽然通常不视为 Smalley 弹性挡圈的典型故障,但在将硬化钢用作凹槽材料时,挡圈剪切可能是一个设计限制。 我们的标准挡圈表中提供了基于挡圈剪切的挡圈轴向负荷能力。 这些值基于建议安全因子为 3 的碳素钢的 剪切强度 。
基于挡圈剪切的 轴向负荷 必须与基于凹槽变形的轴向负荷作比较,以确定设计中的限制因素。
术语
PR = 基于挡圈剪切所允许的轴向负荷 (lb)
D = 轴或外壳直径 (in)
T = 挡圈厚度 (in)
SS = 挡圈材料的剪切强度 (psi)
K = 安全因子(建议值 3)
凹槽变形
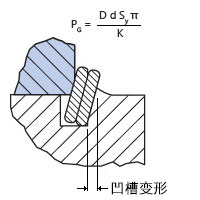 凹槽变形是到目前为止最常见的弹性挡圈设计限制。 当出现永久凹槽变形时,挡圈就开始扭转。 随着扭转角度的增加,挡圈直径开始扩大。 最终,挡圈凹陷并挤出(滚动出)凹槽。 作为一种保守解释,如下等式计算初始凹槽变形点。 在此点位置不会产生故障,故障只在该值非常高时才会发生。 建议采用安全系数 2。 我们的 标准挡圈表中提供了基于凹槽变形的挡圈轴向负荷能力。
凹槽变形是到目前为止最常见的弹性挡圈设计限制。 当出现永久凹槽变形时,挡圈就开始扭转。 随着扭转角度的增加,挡圈直径开始扩大。 最终,挡圈凹陷并挤出(滚动出)凹槽。 作为一种保守解释,如下等式计算初始凹槽变形点。 在此点位置不会产生故障,故障只在该值非常高时才会发生。 建议采用安全系数 2。 我们的 标准挡圈表中提供了基于凹槽变形的挡圈轴向负荷能力。
|
典型的凹槽材料屈服强度 |
|
| 硬质钢 8620 | 110,000 psi |
| 冷拉钢 1018 | 70,000 psi |
| 热轧钢 1018 | 45,000 psi |
| 铝 2017 | 40,000 psi |
| 铸铁 | 10-40,000 psi |
术语
PG = 基于凹槽变形所允许的轴向负荷 (lb)
D = 轴或外壳直径 (in)
d = 凹槽深度 (in)
SY = 凹槽材料的屈服强度 (psi)
K = 安全因子(建议值 2)
凹槽半径
| 轴或外壳直径 | 凹槽底部的最大半径 |
| 1 英寸及以下 | .005 最大 |
| 超过 1 英寸 | .010 最大 |
为了保证最大负载能力,凹槽和弹性挡圈上必须有方角。 此外,弹性组件必须始终与挡圈凹槽成直角,以保持对弹性部分的均匀同心负荷。 凹槽底部的半径应不大于表中所述的值。
弹性组件
最大倒角 = .375 (b-d)
最大半径 = .5 (b-d)
理想的情形是,弹性零件有一个方角,并使挡圈尽可能接近外壳或轴。 弹性零件的最大建议半径或倒角允许值可以使用左边的公式计算。

术语
b = 径向壁 (in)
d = 凹槽深度 (in)
边缘余量
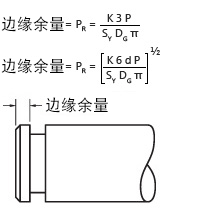 靠近轴端或外壳的挡圈凹槽应有足够的边缘余量以最大化强度。 应检查剪切和弯曲并选择较大值用于边缘余量。 作为一般规则,最小边缘余量可通过 3 倍凹槽深度值得出近似值。
靠近轴端或外壳的挡圈凹槽应有足够的边缘余量以最大化强度。 应检查剪切和弯曲并选择较大值用于边缘余量。 作为一般规则,最小边缘余量可通过 3 倍凹槽深度值得出近似值。
术语
z = 边缘余量 (in)
P = 负荷 (lb)
DG= 凹槽直径 (in)
SY = 凹槽材料的屈服强度 (psi)
d = 凹槽深度 (in)
K = 安全因子(建议值为 3)


关注我们